معمای علوم رایانه که از آن با عنوان Sensitivity Conjecture یا تخمین حساسیت یاد میشود، پس از ۳۰ سال با یک راهحل و اثبات ساده حل شد.
انتشار مقالهای طی ماه جاری که حاوی راهحل مسئلهای به قدمت ۳۰ سال در دنیای علوم رایانه بود، معمایی به قدمت سیسال را در دنیای علوم رایانه با یک راهحل ساده حل کرد. این معما مربوط به تخمینی دربارهی ساختار بلوکهای اصلی به منظور توسعهی مدارهای کامپیوتر است. «تخمین حساسیت» (Sensitivity Conjecture) تاکنون خیلی از دانشمندان سرشناس این حوزه را مقهور خود کرده است؛ اما اثبات جدیدی که بهتازگی برای آن منتشر شده است، بهقدری ساده و پیشپاافتاده است که پژوهشگری خلاصهای از آن را تنها در یک توییت برای دیگران منتشر کرد.
اسکات هارونسون از دانشگاه تگزاس با انتشار پستی در وبلاگ خود در این خصوص گفت:
تخمین حساسیت مورد نظر یکی از خستهکنندهترین و دشوارترین مسائل حلنشده در ترکیبیات و علوم نظری کامپیوتر بوده است.
او در اظهارنظر دیگری دربارهی تخمین حساسیت گفته است:
فهرست افرادی که سعی کردند آن را حل کنند ولی شکست خوردند [درست مانند] فهرست افراد سرشناس در رشتهی ریاضیات گسسته و علوم نظری کامپیوتر است.
حساسیت را یکی از آسانترین روشها برای اندازهگیری پیچیدگی میدانند
تخمین حساسیت مربوط به توابع بولی (Boolean functions) است؛ آنها قاعدههایی برای تبدیل یک رشته از بیتهای ورودی (صفر و یکها) به یک بیت خروجی واحد هستند. یکی از این قاعدهها آن است که بهدست آوردن خروجی «یک» مشروط به آن است که هر کدام از بیتهای ورودی برابر با «یک» باشند. در غیر اینصورت، خروجی صفر خواهد بود. قاعدهی دیگر آن است که اگر تعداد یکهای موجود در یک رشتهی اعداد زوج است، خروجی صفر است؛ در غیر اینصورت، خروجی برابر با یک است. روکو سرودیو (Rocco Servedio) از دانشگاه کلمبیا میگوید:
هر مدار کامپیوتری ترکیبی از توابع بولی است که درواقع همان مواد اولیهی لازم برای انجام هر کاری است که در علوم کامپیوتر انجام میشود.
طی سالها، دانشمندان علوم کامپیوتر راههای زیادی برای اندازهگیری پیچیدگی یک تابع بولی فرضی طراحی کردند. هر کدام از روشها به جنبهی متفاوتی از چگونگی تاثیرگذاری اطلاعات موجود در رشتهی ورودی بر بیتهای خروجی توجه میکند. بهعنوان مثال، «حساسیت» یک تابع بولی تقریبا این احتمال را بررسی میکند که آیا تغییر یک بیت ورودی میتواند بیت خروجی را تغییر بدهد. «پیچیدگی کوئری» نیز محاسبه میکند که برای اطمینانیافتن از خروجی موردنظر، چند بیت ورودی را باید مورد پرسوجو قرار بدهد.

مقالهی مرتبط:
هر کدام از روشهای اندازهگیری، دریچهای منحصربهفرد را بهروی ساختار توابع بولی میگشاید. بااینحال، دانشمندان اکنون دریافتهاند که تقریبا همهی آنها در یک چارچوب یکپارچه میگنجند؛ طوریکه مقدار حاصل از هر کدام را میتوان معیاری تقریبی برای سنجش نتیجهی سایرین دانست. تنها یکی از روشهای اندازهگیری پیچیدگی است که بهنظر میرسد تناسبی با دیگران ندارد: حساسیت.
سال ۱۹۹۲، نوام نیسان (Noam Nisan) از دانشگاه عبری قدس اشغالی و ماریو سزگدی (Mario Szegedy) که اکنون در دانشگاه راتجرز بهسر میبرد، تخمین زدند که حساسیت هم بهخوبی در این چارچوب جا میگیرد؛ اما هیچکس نتوانست این تخمین را ثابت کند. سرودیو میگوید:
میتوانم بگویم که این تخمین، یک سؤال بیجواب مهم در بررسی توابع بولی است.
رایان اُ دانل (Ryan O’Donnell) از دانشگاه ملون نیز دربارهی این موضوع اینگونه اظهارنظر کرده است:
افراد زیادی مقالات طولانی و پیچیدهای نوشتند و سعی کردند [این حدس را] حتی یک گام کوچک بهجلو پیش برانند.
اکنون هائو هوانگ (Hao Huang)، ریاضیدانی از دانشگاه اموری در ایالت جورجیای آمریکا، تنها در دو صفحه تخمین حساسیت را با استدلالی مبتکرانه و درعینحال، ابتدایی دربارهی ترکیبیات نقاط روی مکعبها ثابت کرده است. کلر ماتیو از مرکز ملی تحقیقات علمی فرانسه در مصاحبهای اسکایپی نظر خود را اینگونه بیان کرد:
بسیار زیبا است؛ درست مانند یک مروارید گرانبها.
آرونسون و اُ دانل، هر دو، با اشاره به جملهی معروف پال اردوش (Paul Erdős: ریاضیدان مجارستانی که تعداد مقالاتش در رشتهی ریاضیات، بیشتر از هر شخص دیگری در کل تاریخ است)، دربارهی کتاب مقدسی که خدا اثبات کامل همهی قضیهها را در آن نوشته است، مقالهی هوانگ را «کتاب» اثبات تخمین حساسیت مینامند. آرونسون میگوید:
بهسختی میتوانم تصور کنم که حتی خدا هم بداند که چطور میتوان تخمین حساسیت را با روشی مشابه این حل کرد.
موضوع حساسیت
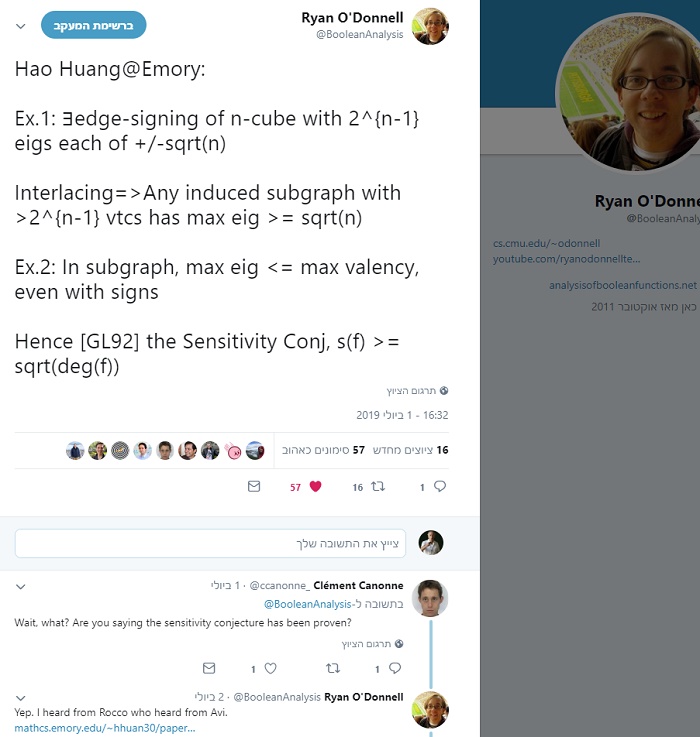
آیا همیشه و درهرحال، نقطهی قرمزی وجود دارد که به نقاط قرمزرنگ دیگر متصل باشد؟
ماتیو برای توضیح این مسئله از یک تشبیه استفاده میکند؛ فکر کنید میخواهید از بانک وام بگیرید و مشغول پاسخگویی به یک سری سوالات بله و خیر هستید. پس از اتمام کار، کارمند بانک به پاسخهای شما امتیاز خواهد داد و خواهد گفت آیا واجد شرایط برای دریافت وام هستید یا خیر. این روند را یک تابع بولی مینامند: پاسخهای شما همان بیتهای ورودی هستند و تصمیم کارمند بانک، بیتهای خروجی فرایند.
اگر با درخواست شما مخالفت بشود، حتما با خودتان فکر میکنید که آیا میتوانستید با یکی دو دروغ در پرسشنامه نتیجه را تغییر بدهید و بهنفع خودتان رقم بزنید. مثلا شاید میتوانستید بهدروغ ادعا کنید که درآمدتان بیشتر از ۵۰ هزار دلار است. اگر این دروغ باعث برعکسشدن نتیجه میشد، درآنصورت دانشمندان علوم کامپیوتر میگویند تابع بولی نسبت به مقدار آن بیت خاص «حساس» است. شرایط دیگری را در نظر بگیرید که هفت دروغ متفاوت میتوانستید بگویید و هرکدام از آنها بهصورت جداگانه بر نتیجه تأثیر میگذارند؛ بنابراین، مقدار حساسیت تابع بولی در فرم درخواست وام شما برابر با هفت است.
حساسیت کلی تابع بولی در علوم کامپیوتر برابر است با بزرگترین مقدار حساسیت در زمان بررسی همهی درخواستهای متنوع و احتمالی وام. بهتعبیر دیگر، این معیار، تعداد سوالاتی را محاسبه میکند که از اهمیتی واقعی در موارد بینابین برخوردار هستند. منظور از موارد بینابین، همان فرمهای درخواست وامی است که اگر کمی [و فقط کمی] فرق داشتند، نتایجشان بهراحتی تغییر میکرد.
حساسیت را معمولا یکی از آسانترین معیارها برای محاسبهی پیچیدگی میدانند؛ اما این معیار فقط یک معیار آموزنده برای روشنگری نیست. بهعنوان کارمند بانک بهجای اینکه از شما بخواهد یک فرم کاغذی را پر کنید، میتواند با شما مصاحبه کند و اینکار را با یک سؤال مشخص شروع کند. سپس، براساس پاسخی که میدهید، سؤال بعدی را طرح کند. هر تعداد سوالی را که او برای رسیدن به تصمیم نهایی مطرح میکند، پیچیدگی پرسش (پرسوجو) در تابع بولی مینامند.
این روش برای اندازهگیری در موارد زیادی کاربرد دارد. بهعنوان مثال، پزشکی میخواهد با کمترین آزمایش ممکن مشکل بیمار خود را حدس بزند، یا اینکه کارشناس یادگیری ماشین میخواهد الگوریتمی بنویسد که برای دستهبندی یک شیء، تاحد ممکن کمترین تعداد از ویژگیهای آن را بررسی کند. بهگفتهی اُ دانل:
شما در خیلی از شرایط، اعم از موقعیتهای پزشکی و موقعیتهای آموزشی، از اینکه قاعدهی زیربنایی [مورداستفادهتان] پیچیدگی کمی در فرایند پرسوجو داشته باشد، واقعا خوشحال خواهید شد.
سایر روشهای اندازهگیری شامل جستوجو برای یافتن سادهترین راه برای نوشتن تابع بولی بهشکل یک عبارت ریاضی یا محاسبهی تعداد پاسخهای احتمالی که کارمند بانک باید به رئیس خود نشان بدهد تا درستی تصمیم خود مبنی بر اعطای وام را ثابت کند، است. حتی یک مدل فیزیک کوانتومی هم از پیچیدگی پرسوجو وجود دارد که در آن، کارمند بانک میتواند ترکیبی «برهمنهی» از چندین سؤال مختلف را در یک زمان مطرح کند. فهمیدن اینکه این روش اندازهگیری چهرابطهای با سایر روشهای اندازهگیری پیچیدگی دارد، به پژوهشگران کمک کرد تا به محدودیتهای الگوریتمهای کوانتومی پی ببرند.
دانشمندان رشتهی کامپیوتر ثابت کرده بودند که همهی این روشها، بهاستثنای حساسیت، رابطهای تنگاتنگ با هم دارند. رابطهی خاصی که در میان آنها وجود دارد، رابطهی چندجملهای است. بهطورمثال، نتیجهی یک روش میتواند توان دوم، توان سوم یا حتی ریشهی توان دوم نتیجهی حاصل از دیگری باشد.
این فقط حساسیت بود که با سرسختی تمام از هرگونه همراهی با این توصیف تمیز و شستهرفته سرباز میزد. بسیاری از پژوهشگران شک داشتند که حساسیت هم واقعا در این چارچوب قرار بگیرد، اما نمیتوانستند ثابت کنند که هیچ تابع بولی عجیبوغریبی وجود ندارد که حساسیت آن رابطهای نمایی (بهجای رابطهی چندجملهای) با سایر روشهای اندازهگیری داشته باشد. و این موضوع به آن معنا است که حساسیت، بسیار کوچکتر از سایرین است. بهقول آرونسون:
این سؤال مانند یک خار ۳۰ سال به چشمان دانشمندان فرو رفته بود.
و بالاخره، رسیدن به راهحل
تخمین حساسیت یکی از خستهکنندهترین و دشوارترین مسائل حلنشده در ترکیبیات و علوم کامپیوتر بوده است
اواخر سال ۲۰۱۲ بود که هوانگ با تخمین حساسیت آشنا شد. او آن دانشجوی فوقدکترا در انستیتو تحقیقات پیشرفته بود و وقت خوردن ناهار با ریاضیدانی بهنام مایکل ساکس از وجود این حدس آگاه شد. هوانگ که بلافاصله به سهولت و ظرافت حدس پی برده بود، میگوید:
از همان لحظه، فکرم بهشدت مشغول آن شد.
هوانگ، تخمین حساسیت را به فهرست محرمانهی مسائل موردعلاقهی خود افزود و هرزمانی که ابزار جدیدی در ریاضیات میآموخت، آن را روی این حدس امتحان میکرد. بهگفتهی وی:
پس از انتشار هر مقالهی جدید، همیشه بهسراغ این مسئله برمیگشتم. البته، پس از زمان معینی آن را کنار میگذاشتم و روی مسائل واقعیتری کار میکردم.
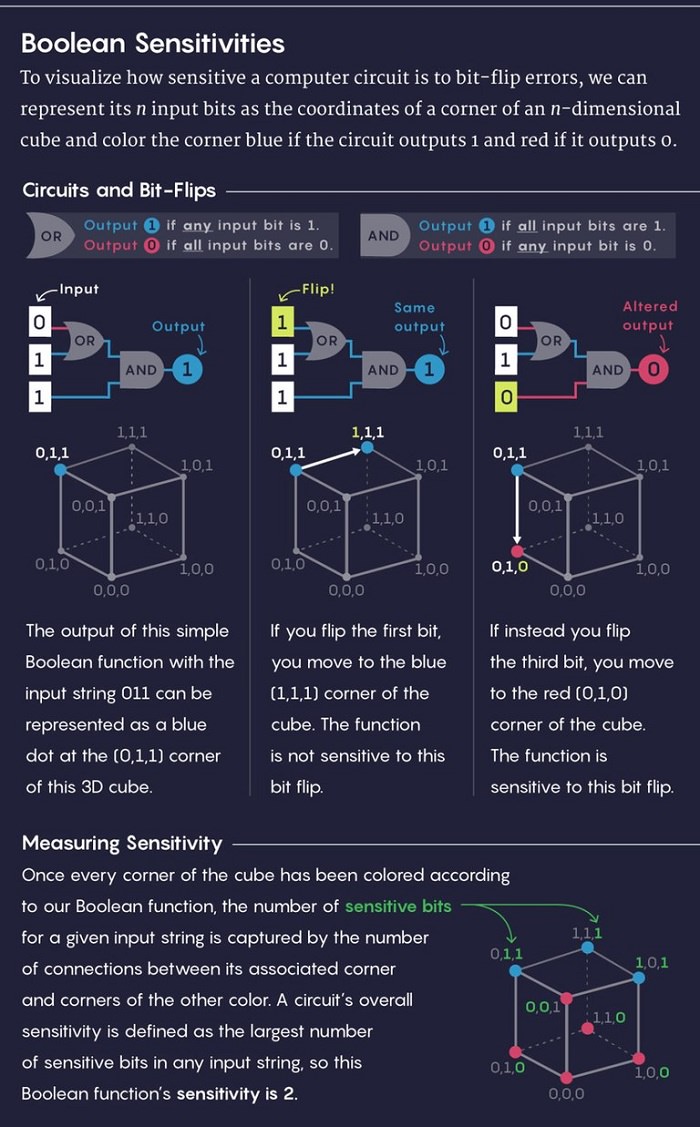
هوانگ پژوهشهای وسیعی در گذشته انجام داده بود و میدانست که تخمین حساسیت را درصورتی میتوان حل کرد که حدسی با تعریف آسانتر دربارهی مجموعه نقاط روی ابعاد مختلف مکعبها ثابت شود. برای رفتن از رشتهای شامل n صفر و یک به سمت نقطهای روی مکعبی n بعدی، یک راه طبیعی وجود دارد: فقط کافی است از n بیت بهعنوان مختصات نقطه استفاده کنید. بهعنوان مثال، چهار رشتهی دو بیتی (شامل ۰۰، ۰۱، ۱۰ و ۱۱) به چهار نقطه از یک مربع در یک پلان دو بعدی اشاره میکند: (۰،۰)، (۰،۱)، (۱،۰) و (۱،۱). بههمینترتیب، هشت رشتهی سهبیتی نیز به هشت گوشه از یک مکعب سهبعدی اشاره میکند و بههمین ترتیب، ابعاد بیشتر میشوند. یک تابع بولی را نیز بهنوبهی خود میتوان بهعنوان قاعدهای برای رنگآمیزی این گوشهها بااستفادهاز دون رنگ متفاوت درنظر گرفت (مثلا، قرمز برای صفر و آبی برای یک).
سال ۱۹۹۲، کریگ گوتسمن، که اکنون در مؤسسهی تکنولوژی نیوجرسی (New Jersey Institute of Technology) بهسرمیبرد، بههمراه ناتی لینیال از دانشگاه عبری قدس اشغالی دریافتند که اثبات تخمین حساسیت را میتوان تا حد پاسخگویی به سؤال سادهای دربارهی مکعبهایی با ابعاد مختلف تقلیل داد: هر کدام از مجموعههایی که بیشتر از نیمی از گوشههای یک مکعب را دربرمیگیرند، انتخاب کنید و آنها را رنگ قرمز بزنید، آیا همیشه و درهرحال، نقطهی قرمزی وجود دارد که به نقاط قرمزرنگ دیگر متصل باشد؟ اینجا، منظور از متصلبودن، آن است که دو نقطهی قرمز به یکی از اضلاع بیرونی مکعب دسترسی داشته باشند و این در تضاد با قرارگرفتن در یک خط مورب است.
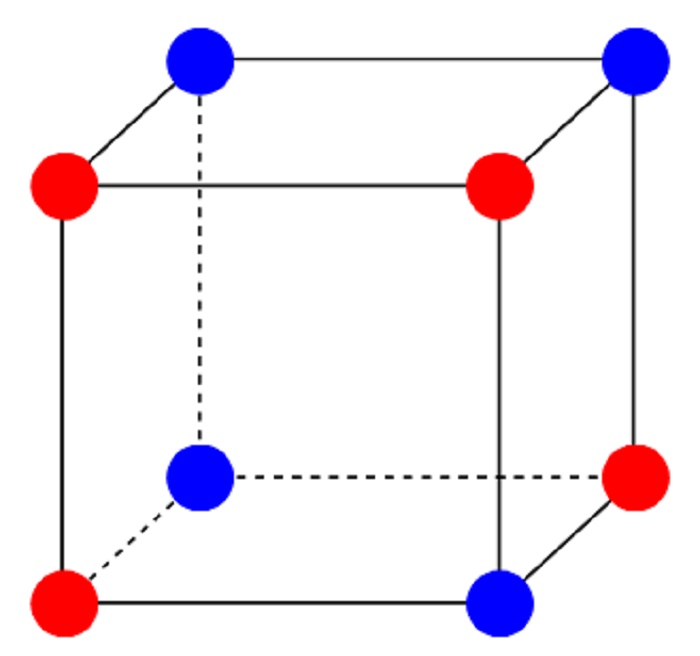
اگر این مجموعه دقیقا شامل نیمی از گوشههای یک مکعب باشد، این احتمال وجود دارد که هیچکدام از آنها هیچ راهی برای اتصال به دیگری نداشته باشند. بهطورمثال، چهار نقطهی (۰،۰،۰)، (۱،۱،۰)، (۱،۰،۱) و (۰،۱،۱) از بین هشت نقطهی موجود در یک مکعب سهبعدی، همگی روی قطر یکدیگر قرار گرفتهاند. اما بهمحض اینکه بیش از نیمی از نقاط روی یک مکعب چندبعدی (با هر تعداد از ابعاد) به رنگ قرمز درآمد، باید چند نقطهی اتصال بین آنها نمایان بشود. حالا سؤال این است: «نحوهی توزیع این اتصالات چگونه است؟ آیا حداقل یک نقطه در بین آنها وجود دارد که به نقاط زیادی متصل باشد؟»
مقالههای مرتبط:
هوانگ سال ۲۰۱۳ بهاین فکر افتاد که بهترین راه برای درک این سؤال همان روش استاندارد برای نمایش شبکهای با ماتریسی است که نقاط متصلبههم را ردیابی میکند و سپس، مجموعهای از اعداد موسومبه مقادیر ویژهی ماتریسی را امتحان میکند. او پنج سال تمام مشغول امتحان اشکال مختلف ایدهی خود بود، اما هیچکدام از راهها به جایی نرسید. او در زیر پستی که آرونسون در وبلاگ خود گذاشته است، نوشته بود که حداقل فایدهی اینکار آن بود که شبهای زیادی به خواب سریع و بیدردسر وی کمک کرده بود.
بالاخره سال ۲۰۱۸ موقعیتی پیش آمد که هوانگ از یک قطعه ریاضی ۲۰۰ ساله بهنام قضیهی درهمبافی کوشی (Cauchy interlace theorem) استفاده كند. این قضیه، ارتباط مقادیر ویژهی ماتریس با مقادیر ویژهی یک زیرماتریس را برقرار میکند و آن را تبدیل به ابزاری عالی برای مطالعهی رابطهی بین یک مکعب و یک زیرمجموعه از گوشههای آن میکند. هوانگ تصمیم گرفت از بنیاد علوم ملی درخواست کمک مالی کند تا بتواند بیشتر این ایده را مورد واکاوی قرار بدهد.
او ماه گذشته، همچنان که در یکی از هتلهای مادرید مشغول نوشتهی درخواست کمکهزینهی خود بود، ناگهان فهمید میتواند با تغییر نشانههای برخی از اعداد موجود در ماتریس خود، این رویکرد را بهسادگی تمام و از هر جهت به ثمر بنشاند. او به این ترتیب توانست ثابت کند که در هر مجموعهای با بیشاز نیمی از نقاط در یک مکعب n بعدی، نقاطی وجود خواهند داشت که حداقل به ریشهی مربع n نقطهی دیگر متصل خواهد بود. تخمین حساسیت هم از همین نتیجه پیروی خواهد کرد.
اولینبار که ماتیو مقالهی هوانگ را در ایمیل خود مشاهده کرد از فرط تعجب صدایی از گلویش خارج شد: «اوه اوه». او انتظار داشت پس از بازکردن مقاله، هیچ چیزی از آن سر درنیاورد:
وقتی عمر مسئلهای به ۳۰ سال میرسد و همه از آن اطلاع داشته باشند، بهاحتمال زیاد اثبات آن یا باید خیلی طولانی، خستهکننده و پیچیده باشد یا خیلی عمیق و پرمعنا.
اما اثبات هوانگ بهقدری ساده بود که ماتیو و خیلی از پژوهشگران دیگر تنها در یک جلسه آن را فهمیدند. ماتیو طی یک پیام اسکایپی ابراز امیدواری کرده است که تدریس آن در دانشگاهها از پاییز همین امسال آغاز شود و بهعقیدهی وی این کار باید تحتعنوان یک موضوع درسی واحد، در گرایش ترکیبیات در سطح کارشناسی ارشد رشتهی ریاضی انجام شود.
هوانگ برای اثبات تخمین حساسیت بسیار قدرتمند عمل کرده است و همین عامل، بیشک پنجرههای جدیدی را بهسمت روشهای اندازهگیری پیچیدگی خواهد گشود. سرودیو فکر میکند حالا با استفاده از این روش میتوان سوالات دیگر مربوط به تجزیهوتحلیل توابع بولی را پاسخ داد و از همه مهمتر اینکه حاصل کار هوانگ توانسته است نگرانیهای بازدارنده دربارهی پرت و ناهمخوان بودن حساسیت نسبتبه جهان متنوع روشهای اندازهگیری پیچیدگی را برطرف کند:
فکر میکنم آن شب پساز شنیدن این خبر، خیلیها راحتتر خوابیدند.
.: Weblog Themes By Pichak :.
