تاریخچهی ریاضیات بدون وجود سوابق نوشتاری، همچنان بهصورت رازی سربهمُهر باقی مانده است. بااینحال، انسانها از چه زمانی مفهوم اساسی عدد را درک کردند؟ حجم و اندازه یا فُرم و شکل را از چه زمانی درک کردند؟ باوجودآنکه هیچکس منشأ درست ریاضیات را نمیداند، ریاضیدانان مدرن میدانند که زبان گفتاری هزاران سال قبل از هر زبان نوشتاری بهوجود آمده است. سرنخهای زبانشناختی وجود دارد که نحوهی بهوجودآمدن تفکر ریاضیاتی در دوران پیش از تاریخ را نشان میدهد.
سرنخهای اولیه
درک تفاوتها درمقایسهبا شباهتها آسانتر است. توانایی تمایز قائلشدن بین کمتر و بیشتر یا مرد و زن یا بزرگتر و کوچکتر، باید مفاهیمی بسیار باستانی باشند؛ اما مفهوم اشیای مختلف که ویژگی مشترکی دارند، مانند سبزی یا گِردی یا خرگوش و پرنده و ماه ویژگیهای مشترک منحصربهفردی دارند که بسیار ظریفتر نیز هستند.
ما واژههای زیادی برای عدد دو داریم که نشان میدهد مفهوم ریاضی «دوتایی یا زوجیّت» پس از اینکه انسانها از زبانی پیشرفته و غنی برخوردار شدند، ممکن است توسعه پیدا کرده باشد. زبان نوشتاری مدتها پس از زبان گفتاری توسعه یافت. متأسفانه بسیاری از سوابق نوشتاری دوران باستان بهمرورزمان از بین رفتهاند.

چوبخطی که در اسکاندیناوی کشف شده است
بااینحال، آثار باستانی که جان سالم بهدر بردند، برخی پیچیدگیهای ریاضی را نشان میدهند. بهعنوان مثال، چوبخطهای باستانی که روی چوب یا استخوان حیوانات حکاکی میشدند، در بسیاری از نقاط دنیا پیدا شدند. هرچند چوبخط ممکن است اثبات شمارش حقیقی نباشد؛ چراکه این ابزارهای پیش از تاریخی بیشتر کاربرد یادآوری و نگهداری سوابق عددی را داشتهاند. باوجوداین، بدیهی است مردمان باستان از مقایسهی یکبهیک بین شکافهای چوبخط و مجموعههایی از اشیای خارجی شاید مانند سنگ و میوه و حیوانات استفاده کردهاند.
اشیای شمارشی
مطالعهی فرهنگهای ابتدایی روزنهی دیگری بهسوی منشأ ریاضیاتی انسانها میگشاید. منظور از ابتدایی، فرهنگی است که در آن، زبان نوشتاری و کتابت و استفاده از ابزارها و فنون مدرن وجود نداشته است. بسیاری از فرهنگهای ابتدایی هنرهای پیشرفته و حسهای عمیق اخلاقی و معنوی داشتند و در جوامع پیچیدهای با قوانین و انتظارات پیچیده زندگی میکردند.
در این فرهنگها، شمارش معمولا با خمکردن انگشتان دست یا اشاره به قسمتهای خاص بدن انجام میشد. مردمان قبیلهای در پاپوآ گینهنو میتوانند با استفاده از انگشتان دست تا آرنج، شانه، دهان و بینی خود از ۱ تا ۲۲ بشمارند. بیشتر فرهنگهای ابتدایی از شمارش شیء خاصی بسته به فراوانی اجسام در محیط اطرافشان استفاده میکردند. بهعنوان مثال، آزتکها از یک سنگ، دو سنگ، سه سنگ و... برای شمارش استفاده میکردند. بدینترتیب، پنج ماهی میشد پنج سنگ ماهی. شمارش در قبیلهای بومی در جاوهی اندونزی با یک دانه آغاز میشود. افراد قبیلهای در نیکای در جنوب اقیانوس آرام نیز از میوه برای شمارش استفاده میکنند.

پلیمپتن ۳۲۲ یکی از اولین جداول مثلثاتی جهان است که بابلیان بهکار میبردند
صورت نوشتاری اعداد امروز هم میتوانسته شمارش شیء خاصی بوده باشد که معنای آن مدتها قبل از بین رفته است. بهعنوان مثال، کلمه پنج نیز احتمالا به دست ارتباطی داشته است. یازده و دوازده هم معانی مشابهی با «یکی بیشتر از» و «دو تا بیشتر از» مجموع انگشتان ۱۰ داشتهاند.
ریاضی که امروزه از آن استفاده میکنیم، «سیستم دهدهی» یا «دستگاه اعداد پایهی ۱۰» است که آن را از یونانیان باستان بهارث بردهایم. بااینحال، فرهنگهای دیگر نیز تنوع زیادی داشتهاند. برخی چینیهای باستان و نیز قبیلهای در آفریقایجنوبی از «سیستم دودویی» یا «دستگاه اعداد پایهی ۲» استفاده میکنند. دستگاه اعداد پایهی ۳ نادر است؛ اما برخی قبایل بومی آمریکا از آن استفاده میکردند. بابلیان باستانی از سیستمی استفاده میکردند که سیستم شمارش شصتتایی یا دستگاه اعدادی برمبنای ۶۰ داشتند. بقایای این سیستم امروزه نیز باقی مانده است؛ بههمیندلیل، در یک ساعت ۶۰ دقیقه و ۳۶۰ درجه در یک دایره داریم.
اعداد نوشتاری
گونههای نوشتاری اعداد از چه زمانی مرسوم شدند؟ بینالنهرینیهای باستان سیستم عددی بسیار سادهای داشتند. در این سیستم، تنها از دو علامت استفاده میشود: یک گُوهی عمودی (v) برای نشاندادن ۱ و یک گُوهی افقی (<) برای نشاندادن ۱۰. بنابراین، این علامت << vvv عدد ۲۳ را نشان میدهد.
مقالههای مرتبط:
بینالنهرینیها هیچ مفهومی بهنام صفر نداشتند. درمقام مقایسه، باید بگوییم این حالت درست بهمانند این است که فرد امروزی نتواند تفاوت بین اعداد ۵.۰۳ و ۵۳ و ۵۰۳ تشخیص دهد. مصریان باستان برای هر ضریب ۱۰ از هیروگلیفهای مختلفی استفاده میکردند. عدد همانطورکه ما نیز امروز از آن استفاده میکنیم، خطی عمودی بود. بااینحال، ۱۰ یک استخوان پاشنهی پا، ۱۰۰ یک طومار یا یک طناب پیچخورده، ۱,۰۰۰ یک گل نیلوفر آبی، ۱۰,۰۰۰ یک انگشت اشاره، ۱۰۰,۰۰۰ یک قورباغه و ۱ میلیون خدای حِح با جهان بالای دوشش بود.
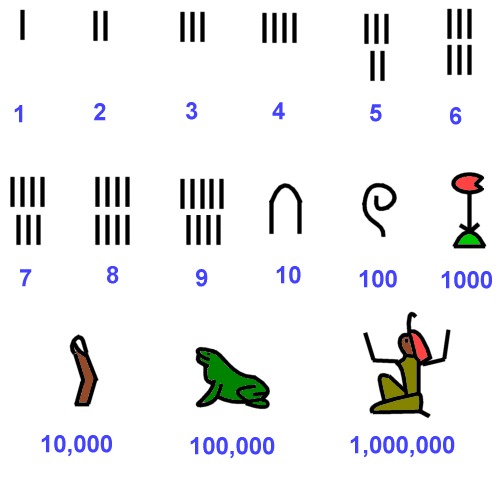
مصریان باستان برای اعداد هر ضریب ۱۰ هیروگلیفهای متفاوتی بهکار میبردند
اعدادی که امروز میشناسیم، در هندوستان توسعه یافتهاند. هندوستان کشوری است که در آن محاسبات و جبر از دیرباز اهمیت بسیاری داشت. در همین کشور بود که اولینبار بسیاری از قوانین مدرن برای ضرب، تقسیم، ریشهی دوم (جذر) و مانند آن بهوجود آمدند.
این مفاهیم بیشتر توسعه پیدا کردند و بهمرور بهوسیلهی دانشمندان مسلمان به جهان غرب برده شدند. بههمیندلیل، نوشتن اعدادی که امروز چه در غرب و چه در شرق (در فارسی و انگلیسی و زبانهای دیگر) استفاده میشود، «عددنویسی هندیعربی» مینامند. بنابراین، هزاران سال طول کشید که انسانها شمارش را آغاز کنند و به دنیای ریاضی پای بگذارند.
.: Weblog Themes By Pichak :.
